ჩაქუჩიპირველ რიგში მადლობა იმისათვის რომ თემას პერიოდულად აცოცხლებ
როგორც თავიდანვე დავწერე, პერიოდულად როცა საქმეები მიგროვდება იმდენ ყურადღებას ვეღარ ვუთმობ ხოლმე, მაგრამ როგორც კი თავისუფალი დრო გამოჩნდება ვეცდები მეტი და მეტი მასალა დავდო.
user8855 საქართველოში არ ვარ მე თვითონ

ისე კი, მეც ვატყობ რომ სულ უფრო და უფრო მეტი ხალხი ცდილობს პითონის სწავლას და ძალიან მიხარია
ტაკს, გადავედით უშუალოდ საქმეზე:
უხეშად რომ ვთქვათ რეკურსიული ეწოდება ფუნქციას, რომელიც იძახებს თავის თავს.
ხანოის კოშკები არის კლასიკური ამოცანა, რომელიც იხსნება რეკურსიის გამოყენებით (იხ. სურათი):
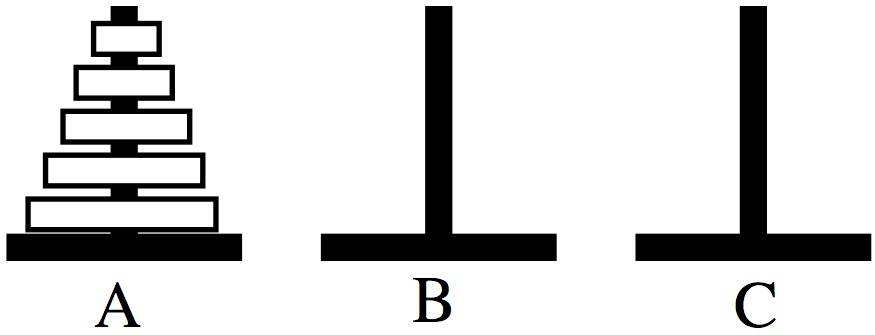
გვაქვს სამი ღერძი. ერთერთზე ჩამოცმულია სხვადასხვა ზომის N ცალი რგოლი, რომლებიც ერთმანეთზე ზომის მიხედვით ისეა დალაგებული, რომ ნებისმიერ რგოლს ზემოდან მასზე მცირე ზომის რგოლი ადევს.
ჩვენ შეგვიძლია ერთ ჯერზე ავიღოთ ნებისმიერ ღერძზე განლაგებული რგოლებიდან სულ ზედა რგოლი და გადავიტანოთ ნებისმიერ სხვა ღერძზე იმ პირობით თუკი ამ რგოლს დავდებთ მასზე ზომით უფრო დიდ რგოლზე, ან ცარიელ ღერძზე.
მაგალითად სულ თავიდან ყველა რგოლი განლაგებულია ისე, როგორც ეს სურათზეა ნაჩვენები. პირველ სვლაზე შეგვიძლია ავიღოთ სულ ზედა რგოლი და გადავიტანოთ ნებისმიერ ღერძზე. შემდეგ სვლაზე შეგვიძლია ავიღოთ მეორე რგოლი და გადავიტანოთ თავისუფალ ღერძზე, იმიტომ რომ იმ ჩვენს პატარა რგოლს თავზე ზემოდან ვერ დავადებთ ამოცანის პირობიდან გამომდინარე.
ამოცანა მდგომარეობს შემდეგში -
სვლების რა მინიმალური რაოდენობაა საჭირო მთლიანი პირამიდის A ღერძიდან B ღერძზე გადასატანად?სიმარტივისთვის ავიღოთ ის შემთხვევა როდესაც გვაქვს მხოლოდ 3 რგოლი და ზომების მიხედვით დავარქვათ პირობითად 1, 2 და 3.
მაშინ პირვანდელი მდგომარეობა შემდეგნაირად გამოიყურება:
a=[3, 2, 1] - ანუ რგოლები ერთმანეთზე დალაგებულია მარცხნიდან მარჯვნივ მიმდევრობით. სულ პირველი დევს 3-იანი, მას ზემოდან ადევს 2-იანი და ბოლოს 1-იანი.
b=[]
c=[]
პირველ სვლაზე ავიღეთ 1-იანი და გადავიტანეთ b ღერძზე, მივიღეთ:
a=[3, 2]
b=[1]
c=[]
მეორე სვლაზე ავიღეთ 2-იანი და გადავიტანეთ c-ზე:
a=[3]
b=[1]
c=[2]
#3 - 1-იანი ავიღეთ b-დან და გადავიტანეთ c-ზე:
a=[3]
b=[]
c=[2, 1]
#4 - 3-იანი გადავიტანეთ b-ზე:
a=[]
b=[3]
c=[2, 1]
#5 - 1-იანი გადავიტანეთ a-ზე:
a=[1]
b=[3]
c=[2]
#6 - 2-იანი გადაგვაქ b-ზე:
a=[1]
b=[3, 2]
c=[]
#7 - 1-იანი გადაგვაქ b-ზე:
a=[]
b=[3, 2, 1]
c=[]
როგორც ვხედავთ დაგვჭირდა 7 სვლა იმისათვის, რომ 3 რგოლი A ღერძიდან B ღერძზე გადაგვეტანა.
რაც შეეხება ამოხსნას, ვიდრე უშუალოდ კოდს შევეხებოდეთ ჯერ გავარჩიოთ როგორ ვხსნით ამ ამოცანას თეორიულად. დედუქციის დახმარებით შეგვიძლია ვთქვათ შემდეგი - თუკი ჩვენ მოვახერხეთ სულ ქვედა, ყველაზე დიდი რგოლის გარდა ყველა სხვა დანარჩენი რგოლის გადატანა ე.წ. "დამხმარე" ღერძზე (ანუ თუკი A-დან B-ზე უნდა გადავიტანოთ, ამ შემთხვევაში C ღერძი არის დამხმარე), მაშინ ჩვენ შეგვიძლია ეს ყველაზე დიდი რგოლი გადავიტანოთ დანიშნულების ღერძზე და ჩემდეგ დამხმარე ღერძიდან იგივე მოქმედებით გადმოვიტანოთ დანარჩენი რგოლები და დავადოთ ამ დიდ რგოლს.
რეკურსია ამ შემთხვევაში გამოიყენება სწორედ რომ იმ ზედა რგოლების დამხმარე ღერძზე და შემდეგ დანიშნულების ღერძზე გადასატანად. ჩვენ ვამბობთ რომ ის ზედა რგოლები ჩვენთვის იგივე პირამიდაა და დამხმარე ღერძი არის სინამდვილეში დანიშნულების ღერძი, და ფაქტიურად გვაქვს იგივე ამოცანა, ოღონდ ახალი, შედარებით მარტივი მოცემულობით - თუკი მთავარ ამოცანაში გვჭირდება N რგოლის გადატანა A-დან B-ზე, ამ ახალ ამოცანაში გვჭირდება N-1 რგოლის გადატანა A-დან C-ზე.
ანუ მთავარი ამოცანა დავიდა შემდეგზე:
სვლა #1 - N-1 რგოლის გადატანა A-დან C-ზე
სვლა #2 - ბოლო, ყველაზე დიდი რგოლის გადატან B-ზე
სვლა #3 - N-1 რგოლის გადმოტანა C-დან B-ზე
თავის მხვრივ #1 და #3 ამოცანები ისევ შეგვიძლია გავამარტივოთ:
#1:
#1.1: (N-1)-1 რგოლის გადატანა A-დან B-ზე,
#1.2: (N-1)-ე რგოლის (ამ შემთხვევაში ეს რგოლია ყველაზე დიდი) გადატანა A-დან C-ზე
#1.3: (N-1)-1 რგოლის გადატანა B-დან C-ზე
შემდეგ მთავარი ამოცანის მე-2 სვლა:
#2: მე-N ყველაზე დიდი რგოლის გადატან B-ზე
და მე-3 სვლა ანალოგიურად ჩაშლილი:
#1.1: (N-1)-1 რგოლის გადატანა C-დან A-ზე,
#1.2: (N-1)-ე რგოლის (ამ შემთხვევაში ეს რგოლია ყველაზე დიდი) გადატანა C-დან B-ზე
#1.3: (N-1)-1 რგოლის გადატანა A-დან B-ზე
და დანარჩენი სვლებიც უნდა ჩაიშალოს მანამდე, სანამ ხელში არ შეგვრჩება მხოლოდ 1 რგოლი.
კოდი გამოიყურება შემდეგნაირად:
ტიპებმა ქვეყნის მომავალი ლომბარდში ჩადეს ფული მოტეხეს და ვალდებულებებს ჩვენ გვიტოვებენ


