რამდენიმე კითხვა ფიზიკოსებს, III კანონი

ZAZAi

ვაახ, ვეღარ გავიგეთ რა გინდათ.
ზღვრულიაო - რატოა ზღვრულიო.
აგერ, ნეიტრინომ ხომ გადააჭარბა - ხოდა გვაცალეთ დადასტურება. მინამ კარგად არ შემოცმდება - არ მიიღება.
მორჩა, იეღოვას ასე სურს

მე საერთოდ მეეჭვება რამეს შემოუსაჭღვრელს/უსასრულოს ფიზიკური შინაარსი ჰქონდეს. რავი აბა

ნეტრინოს რაც შეეხება:

და მაინც, საინტერესო მოსაზრებები/თეორიებ იფრქვევა ყოველ მხრიდაან

asphurcela

ესეიგი, ექსპ ფუნქცია არ უნდა მივუყენოთ კონდესატორს. ფორმულა, რომელიც მე შემოგთავაზეთ, გამოვიყვანე, კიარ დამსიზმრებია. აქამდე იმიტომ არაფერი დავწერე, რომ ორშაბათი იყო (ცრუმორწმუნე ვარ, ორშაბათობით სახლში ვიკეტები და ვცდილობ არაფერი გავაკეთო ხომე). იმის დამტკიცებაც ვიცი, თუ რატომ არ უნდა მივუყენოთ ექსპ ფუნქცია კონდესატორს:
გამოვთვალოთ კონდესატორიდან გამოსული მუუხტი q=CUmax-CUmin; ამ უხტის გამოსვლისას შესრულდა მუშაობა, რომელიც ტოლია A=CUmax^2/2-CUmin^2/2; არსებობს ფორმულა A=qU; აქედან A და q ვიცით და U საშუალოს პოვნა არ გაგვიჭირდება; თქვენ რომ U საშუალოს დასადგენად გამოთვლით ექსპ ფუნქციის განსაზღვრულ ინტეგრალს, იგივე მნიშვნელობას ვერ მიიღებთ მაგალითად, შემდეგი პირობებისთვის:

ფორმულის საბოლოო სახის მისაცემად ვიყენებ შემდეგ ფორმულას q/t=U/R; აქდან მთავარი U საშუალოს პოვნა იყო, ხედავთ რა მარტივია ყველაფერი.
ასფურცელა ალბათ იტყვის, ველოსიპედი ბორბლიანი გამოდგაო.

Komponent
მერე ეგ საშუალო ძაბვა სულ სხვა რამეა და ექსპონეტის მეშვეობით გამოთვლილი სულ სხვა - ექსპონენციალურ კანონში დროითი ევოლუციაა დათვლილი; რამდენადაც არ უდნა უკირკიტოთ ამ ყველაფერს, ფიზიკა სწორედაც რომ არაფერ შუაშია, მათემატიკურად გამოდის ეგრე, მკაცრი დამტკიცებით და არა ჩხირკედელაობით. ასევე არასწორია ფორუმულა q/t = U/R, მანდაც მათემატიკური სიმკაცრე მოითხოვს ინტეგრალი გამოიყენოთ და არა საშუალო ძაბვის მნიშვნელობა.

This post has been edited by Irakli on 22 Nov 2011, 01:06

Komponent
რა კარგი ადამიანი ხართ, ვერც კი წარმოიდგენთ
ხო, ეგ ველოსიპედი ბორბლებიანია, ოღონდ ოთხკუთხედი ბორბლებით
კი ბატონო, ისარგებლეთ მაგ ფორმულით.
რაც მთავარია, თქვენს კალკულატორს ადვილად გამოიყენებთ.
მე და მილიონობით ინჟინერი ისევ ძველი ფორმულით ვიხლაფორთებთ

ამ ეტაპზე, შეიძლება რაღაცას სწორად ვერ ვაკეთებ, ამ ეტაზე თქვენც ნუ იქნებით ძალიან კატეგორიულები, ხომ ხედავთ აინშტაინს და სინათლის სიჩქარესაც უტევენ. ვგრძნობ რომ ახლოს ვართ სიმართლის გარკვევასთან და ახლა გვმართებს მაქსიმალური ზრდილობა.
მივმართოთ ისევ კრიტიკულ აზროვნებას:
ერთი თქვენი მინუსი ის არის, რომ რეაქცია ეგრევე გააკთეთ, თუმცა ასფურცელა ბევრს იცინოდა,– მაგრამ ეს მაინც ზოგადი ლაპარაკია, მოდით ვიმსჯელოთ, ვიდისკუსიოთ, იქნებ რამეს მივაღწიოთ.
ფიზიკა და მათემატიკა ერთნაირად მკაცრები არიან, მე რომ საშუალო ძაბვას ვითვლი, პირდაპირ ენერგიის მუდმივობის კანონიდან მოდის, ინტეგრალიც საშუალოა, სხვა რამე კი არ არის. ინტეგრალს სავარაუდოდ სწორად ითვლით, საეჭვო ის არის, რომ ეგ ექსპ ზუსტად აღწერს კი კონდესატორს?
Irakli

და მერე სად არის ეგ მკაცრი დამტკიცებები, იქნებ რამე შევამჩნიო, აგრეთვე უფრო წვრილად გააკრიტიკეთ ჩემი მტკიცება, იქნებ აქაც შევამჩნიო რამე.
რათქმაუნდა ასფურცელას ვეტყვი, რომ ადამიანთა რაოდენობის მოშველიება არასპორტული საქციელია
ყველანი ადამიანები ვართ, ყველას შეიძლება შეეშალოს, თვით აინშტაინებსაც კი.–ეს ფიზიკოსის ერთერთი ზრდილობაა.
მე თქვენ მომწონხართ, რაც გასწავლეს იმიღეთ და ჩემსავით კრიტიკა, კირკიტი და ჩათლახობა არ დაგიწყიათ

Komponent
ვერაფერი ვერ გავიგე რაც ზედა პოსტში გიწერიათ.
ეგებ ჩამოაყალიბოთ რას ითხოვთ "ჩვენგან"?

რას ვითხოვ და დავამტკიცოთ სიმართლე, კონდესატორს, ექსპ-სა და ჩემ მიერ დაწერილ ფორმულას შორის, რათქმაუნდა თუ შეგიძლიათ ან ვინმეს თუ შეუძლია. ეჭვებში ვართ ბევრი (ჩემს გარშემო)-ეს რა წამოვიწყე თქვენ თუ არხეინად ხართ ამ საკითხთან დაკავშირებით, ჩვენც გვასწავლეთ როგორ უნდა ვიყოთ არხეინად.

Komponent
რავიცი, რამე სახელმძღვანელო უნდა აიღოთ და გაიაროთსრლი კურსი, დაკვირვებით.
დამტკიცება თუ გნებავთ, ხვალ დაგიმტკიცებთ. ეხლა არ ვზივარ კომპტან, ტელეფონიდან ვპოსტავ დაძნელია ბეჭვდა

კი რათქმაუნდა, დამტკიცება მინდა, მადლობელი დაგრჩებით.

პირველ რიგში გილოცავთ გიორგობას.
ეხლა, ფიზიკას მივხედოთ

Komponent

არა, არხეინად ვერ ვიჯდებით. სხვა გაცილებით უფრო რთული თავსატეხები გვაქვს. ამიტომ 99% ფიზიკოსებისა დაკავებულია და ფორუმზე მხოლოდ ძალიან უმნიშვნელო რაოდენობრივი ნაწილი შემოდის.

ოკ. გამოვიყვანოთ RC წრედის განტოლება და ვაჩვენოთ საიდან ჯდება ექსპონენტა. ეგებ დაესიზმრა ვიღაცას და მას მერე არავინ დაინტერესებულა.
მაგრამ ეს განტოლება იმდენად მარტივად გამოდის, რომ მეტი არც კი შეიძლება. 2+2 ის დონეზეა ფიზიკაში.
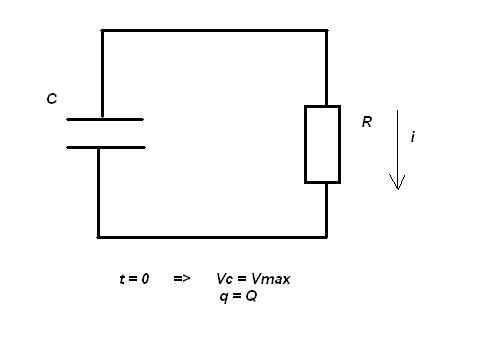
იხილეთ თან დართული ნახატი.
გვაქვს კონდენსატორი პარალელურად მიერთებული წინაღობასთან.
საწყისი პირობებია t=0 მომენტში, კონდენსატორზე ძაბვა Vc = Vmax რაღაც მაქსიმალურ მნიშვნელობაზეა დამუხტული.
მასზე საწყისი მუხტი არის Q და დროის მიხედვით ის განიმუხტება რეზისტორზე. ეს დროზე დამოკიდებული მუხტი აღვნიშნოთ პატარა q- თი.
შევხედავთ ნახაზს და ვწერთ მარტივი კირხოფის წესით ძაბვების მნიშვნელობებს:
Vc + Vr + 0 = 0
აქ მესამე წევრად 0 სპეციალურად დავწერე, რადგან, როცა კვების წყაროა ჩართული, მაშინ ამ 0-ის მაგივრად მისი ელ-მამოძრავებელი ძალა (კვების ძაბვა) იწერება ხოლმე. რადგან არ გვაქვს, უბრალოდ 0 ზის ახლა.
ე.ი. Vc + Vr =0
Vc = -Vr
Vc = - i * R [1] (რეზისტორზე ძაბვა წარმოვადგინე დენისა და წინაღობის სახით. კვადრატული ფრჩხილები ფორმულის ნომერს აღნიშნავს)
განმარტების თანახმად, კონდენსატორის ტევადობა C = q/V (ასე შეთახმდნენ, რომ მოდით ავდგეთ და კონდენსატორზე რა მუხტიც გვაქვს ის შევაფარდოთ მასზე ძაბვას და დავარქვათ ტევადობა)
ე.ი. Vc = q/C
ასევე, კონდენსატორში გადის დენი, როცა მასზე მუხტი იზრდება ან იკლებს, ანუ იცვლება. სხვა შემთხვევაში დენი უდრის 0-ს.
ანუ: i = dq/dt (მუხტის ცვლილება დროში არის დენი).
ჩავსვათ ეს ყველფერი [1] განტოლებაში:
q/C = - R * dq/dt (გადავაჯქუფოთ, q -ები ერთ მხარეს, დანარჩენი მეორე მხარეს)
(1/q)*dq = - (1/RC) * dt [2]
ავიღოთ ინტეგრალი ორივე მხარეს. (ინტეგრალი 1/x -დან არის ln(x)+constan)
ln(q)+constant = -(1/RC) * t [3]
საჭიროა ვიპოვოთ ახლა ინტეგრირების მუდმივა. ამისთვის ვიყენებთ საწყის პირობებს:
როცა t = 0 , მაშინ Vc = Vmax და q = Q.
ჩავსვათ ესენი [3]-ე ფორმულაში:
ln(Q) +constant = -(1/RC) * 0
ln(Q )+constant = 0
constant = ln(Q)
ვიპოვეთ ეს მუდმივა და ჩავსვათ [3]-ში:
ln(q) - ln(Q) = -(1/RC) * t (ლოგარითმის თვისებების გამოყენებით):
ln(q/Q) = -(1/RC) * t
რაც იგივეა, ისევ ლოგარითმის წესებიდან:
q/Q = exp(-(1/RC) * t)
q = Q * exp(-(1/RC) * t) [4]
ესაა საბოლოო ამოხსნა. აქედან გვინდა ძაბვაზე გადავალთ გვინდა დენზე:
q = Vc * C განმარტებით და საწყისი პირობით, რომ Q = Vmax * C:
Vc * C = Vmax * C * exp(-(1/RC) * t)
Vc = Vmax * exp(-(1/RC) * t)
იგივენაირად გადავალთ დენზეც q = i*t განმარტებიდან გამომდინარე.
სულ ესაა.

This post has been edited by asphurcela on 23 Nov 2011, 17:42

მიმაგრებული სურათი

მეც გილოცავთ გიორგობას
მადლობელი ვარ ვრცელი პასუხისათვის,
განხილულ თემასთან დაკავშირებით, სანამ ჩემ პასუხს გამოვაქვეყნებ იქნებ კიდევ ერთხელ დაამეხმაროთ და მითხრათ ქოვემოთ მოყვანილი ფორმულის ინტეგრალი თუ არსებობს და თუ არსებობს რა არის.
e^(-t/RC)

კი არსებობს:

ინტეგრალი (exp(-t/RC))dt = -R*C*exp(-t/RC)+constant
აქ იტეგრება გავაკეთეთ t-ს მიმართ.
მუდმივა ყოველთვის დაჯდება. მისი პოვნა კი კონკრეტულ ამოცანაზე და საწყის პირობებზეა დამოკიდებული

GeorgeSword

ელექტროდინამიკაში სინათლის კვანტი არის თვითონ ურთიერთქმედების გადამტანი.
და ის საზღვრავს ნაწილაკების სიჩქარეს....
რომელ ზღვრულ სიჩქრეზე ლაპარობ? და ნეიტრინო რა შუაშია?

შენ თვითონ თუ გესმის ამ წინადადების აზრი? უაზრობა რომ არის თუ გრძნობ?

This post has been edited by vasovasia on 24 Nov 2011, 03:31

vasovasia

სამწუხაროდ ძალიან ადვილად გამოგვაქვს დასკვნა, არ დაგიდევთ კარგად ვართ თუ არა გარკვეული მოცემულ საკითხში თუ ამოცანაში...

იმედი მაქვს ეს მარტო ქართველებს არ გვახასიათებს...

This post has been edited by nforumi on 24 Nov 2011, 12:31