არწივი9არაა სულ სხვა სფერო
ალგორითმია უბრალოდ და კომპში უშვებ ჩვეულებრივად
პერცეპტრონზე რაც გაქვს ის რომ აიღო და და ბევრი შრეები დაამატო შუაში აქტივაციის ფუნქციებით ეგაა,
უბრალოდ პერცეპტრონის სწავლის ალგორითმი სხვანაირია თუ სწორად მახსოვს, backpropagation (უკუგავრცელება?) გამოიყენება ნეირონულ ქსელებში.
ცუდად ვიცი ახსნა და საკმაოდ არატექნიკურად მაგრამ ეს შედეგი მივიღე:
მოკლედ ძალიან ძალიან რომ გავამარტივო, რაღაც ინფორმაცია შედის ნეირონულ ქსელში,
მაგალითად შედის ოთახების რაოდენობა და ფართობი, და უნდა გამოიცნოს ფასი,
ორივეს რაღაც კოეფიციენტებზე ამრავლებს და ჯამავს
ხოდა შემთხვევითი წონები/კოეფიციენტები ხომ არ მოგცემს არა სწორ პასუხს?
ხოდა ამიტომ ფუნქციას წერ, მაგალითად, სიზუსტე = (Y-y)^2 სადაც Y არის ნამდვილი ფასი სახლის, y კიდე ჩვენი კოეფიციენტებით მოცემული
ანუ ჩვენ ახლა შეგვიძლია კალკულუსის გამოყენებით ამ ფუნქციაში ჩვენი წონებისთვის დავთვალოთ ე.წ. partial derivative, წარმოებული(არ ვიცი partial derivative ქართულად :დ) ამ სიზუსტის ფუნქციის მიმართ,
ხოდა რეალურად ხომ წარმოებული არის მხები რომელიც გადის ფუნქციაში კონკრეტულ წერტილზე არა? და მისი ნიშნით/სიდიდით შეგიძლია განსაზღვრო ეგ კოეფიციენტი როგორ შეცვალო რომ შენი სიზუსტე გაზარდო ან შეამცირო, ანუ შეგიძლია წონები "ისწავლო". მაგრამ რახან y = ax1 + bx2 + c წრფივი ფუნქციაა მას ვერ ასწავლი არაწრფივ დამოკიდებულებას , (a და b რომ იყოს კოეფიციენტები და x1, x2 იყოს ოთახის რაოდენობა და ფართობი, c კიდე თავისუფალი წევრი რომ სიბრტყეზე "ზემოთ-ქვემოთ" ამოძრაოს ეს წრფე)
ამის გაზოგადება შეიძლება როცა როცა მხოლოდ y = ax + b კი არ გვაქვს არამედ ax1 + bx2 +.... cxn +b გვაქვს და ზუსტად იგივენაირად ისწავლის მაგრამ მხოლოდ წრფივ დამოკიდებულებას ვიღებთ მაინც.
ამიტომ ამ წრფივ ფუნქციაში ატარებენ ბევრჯერ, მაგრამ წრფივ ფუნქციას რომ წფივ ფუნქციაში გაატარებ ჯამში ხომ მაინც წრფივი გარდაქმნა გამოდის არა? და უფრო რთულ რამეს ვერ ისწავლის რამდჯერაც რამე ახალი კოეფიციენტები არ უნდა დაუმატო,
ამიტომ შემოაქვთ არაწრფივი ელემენტი, მაგალითად შედეგს ატარებენ tanh ში
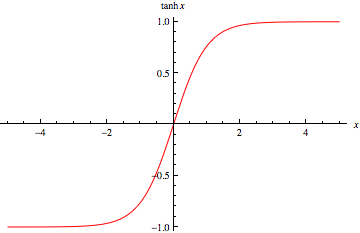
მერე უკვე თავიდან მიდის იგივე პროცესი
და რაც უფრო მეტი შრეა მით უფრო რთული დამოკიდებულებების სწავლა შეუძლია
თეორიულად დამტკიცებულია რომ ნებისმიერი ფუნქციის/დამოკიდებულების სწავლა შეუძლია
ხოდა ამდენი სამეცნიერო ნაშრომი რომ გამოდის ამ თემაზე უმრავლესობა ამ მარტივ პრინციპებს ეფუძნება და უფრო კონკრეტულად იმ კითხვებზე პასუხობს რომ რა არის კარგი საწყისი კოეფიციენტები/წონები(როგორ უნდა შეირჩეს), gradient ს რომ დავითვლით( partial derivative ების ვექტორი) უფრო კონკრეტულად როგორ გამოვიყენოთ ის წარმოებულები კოეფიციენტების შესაცვლელად რომ უკეთესად ისწავლოს ქსელმა, და ა.შ.
მოკლედ ტექნიკებზეა რა და მათემატიკურად თუ ამტკიცებენ მაშინ ხომ ვაბშე მაგარი ნაშრომია თუ არადა უბრალოდ ექსპერიმენტულად თუ ბევრი რაღაც სცადეს და რაღაცამ არსებულ შედეგებზე კარგი შედეგი დადო მაინც კარგად დაფასდება ნაშრომი :დ
This post has been edited by execution on 22 Aug 2018, 01:22
ხელოვნური ინტელექტი, მიღწევები, სიახლეები.
თბილისის ფორუმი -> თემატური ფორუმი -> მეცნიერება და განათლება -> ტექნიკური და საბუნებისმეტყველო მეცნიერებები
