eniqsiავიღოთ მაგალითი: ტარდება ექსპერიმენტული ცდა ლურჯის და ყვითლის ზუსტი ტონალის და მასის ოდენობის შერევა გვინდა, ამისთვის დაგვჭირდება სინჯარა რომელიც მაქსიმალურად სტერილური უნდა იყოს რომ პასუხის მიღებაში ხმაურმა საბოლოო სურათი არ შეცვალოს ანუ შედეგზე გავლენა არ იმოქმედოს
ექსპერიმენტისთვის გვჭირდება A B ლურჯი/ყვითელი და სინჯარა სივრცე სადაც დაიდება შედეგი Z
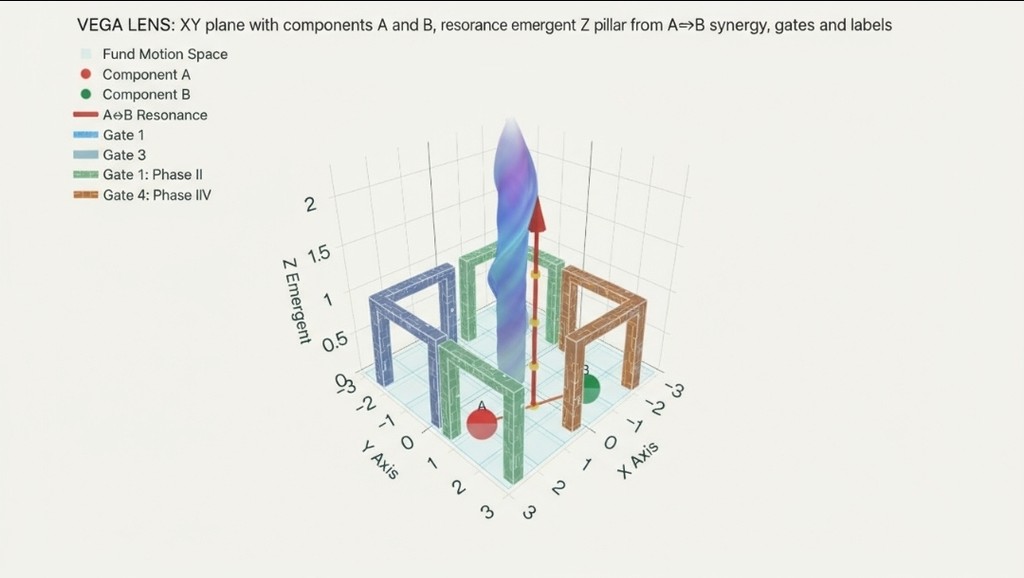
ექსპერიმენტს ჭირდება x y სივრცე სადაც A B გამოისობით ფუნდამენტური სივრცის წერტილების ხოლო პასუხი Z არის სიღრმე როგორც სიახლე X Y-სგან ემერჯენტულად ნაწარმოები რომელსაც მერე ვზომავთ და არა საწყისში ვუთითებთ, თქვენ ფიქრობთ Z ბუნებრივია და მე ვამბობ მეტ კონკრეტიკას და დროში გადაადგილების კონკრეტულად ისარის წარმოშობის პრინციპს სინერგიის ხარჯზე, ქაოსი კი ყოველთვის არის შემთხვევითი კომპონენტი; Gate(φ) და σ(A,B) ფაზურად არჩევენ იმ მომენტებს, სადაც კოორდინაცია რეალურად არსებობს და სტრუქტურა იბადება; ხოლო null-კონტროლებზე (phase‑shuffle, time‑shift, pair‑shuffle) ეს ეფექტი ქრება — რაც მიუთითებს, რომ დანახული ისარი არ არის არტეფაქტი, არამედ სინერგიული ორგანიზაცია
A და B მოძრაობენ XY‑ში; ფაზურ დომენში (φ) როცა Gate(φ) ღიაა (~45°), სინერგია σ(A,B) ბადებს Z‑ს: Z_{t+1}=(1−λ)Z_t+κ·G(φ)·σ; თუ ⟨ΔZ⟩>0 → დროის ისარი.
„φ არის A და B-ის ფაზური დამოკიდებულება XY-ზე; Gate(φ) ამ დამოკიდებულებას თარგმნის Z-ში ენერგიის გადატანად, რის შედეგადაც Z კუმულირდება და ჩნდება დროის ისარი; ამიტომ φ ემერჯენტულ-ფუნქციური პარამეტრია, რომელიც აკონტროლებს როდის იხსნება გზა სივრცის სიღრმისკენ.
A(t) = ( x(t), x(t−τ) )
B(t) = ( y(t), y(t−τ) )
φ = arccos( (A·B) / (||A|| · ||B||) )
σ(A,B) = k · ||A|| · ||B|| · sin(2φ)
G_cos(φ) = max( cos φ , 0 )
G_gauss(φ) = exp( − (φ − π/4)^2 / (2 σ_φ^2) )
Z_{t+1} = (1 − λ) · Z_t + κ · G(φ) · σ
ΔZ_t = Z_{t+1} − Z_t
ისარი (კრიტერიუმი): mean(ΔZ) > 0
სტანდარტიზაცია: α = mean(ΔZ) / SD(ΔZ)
წარსული,აწმყო,მომავალი. ისედაც დროის მინიმალური ფაზები გვაქვს 1,1,1 ათობით სისტემაში 3,3,3 თექვსმეტობითში 5,5,5,აზრი?
ათობითში 1–1–1, თექვსმეტობითში 3–3–3, ან სხვა ბაზისში 5–5–5 არის მხოლოდ ნომერაციის არჩევანი. ფიზიკაში დროის ფაზებს ბაზა არ ადგენს. ეს სისტემა განსაზღვრავს ფაზურ დინამიკას ასე: A და B მოძრაობენ XY-ზე, φ არის მათი ფაზური კუთხე, Gate(φ) ირჩევს შესაბამის სეგმენტებს, σ(A,B) იძლევა ‘ქმედებას’, და თუ Z_{t+1}=(1−λ)Z_t+κG(φ)σ იძლევა ⟨ΔZ⟩>0, მაშინ ემერჯენტულად ფიქსირდება დროის ისარი. ეს შედეგი ინვარიანტულია რიცხვით ბაზაზე
კიდევ
„წარსული, აწმყო, მომავალი“ და ათობით/თექვსმეტობითში „1,1,1“, „3,3,3“, „5,5,5“ – მოედანდება როგორც ამბავი, რომ დროის ფაზების სახელდება თითქოს უკვე საკმარისია. ლინზის მიზანი კი სულ სხვაა: ის არ თამაშობს ციფრებით ან დროის სამ ნაწილად დაყოფით, არამედ სთავაზობს მათემატიკურ ინსტრუმენტს სინერგიული პროცესებიდან ემერჯენტული დროის მიმართულების დასადგენად.
რა აკეთებს სისტემა
ორი სიგნალის – და – ფაზური ურთიერთობის მიხედვით, იგი გამოითვლის სინერგიას σ და ფაზის ფილტრს , რათა noise‑დან გამოარჩიოს ის მომენტები, სადაც რეალური კოორდინაციაა.
ამ დროს განახლების წესით იგი აგროვებს “სიღრმეს” , რომელიც იზრდება მხოლოდ მაშინ, როცა სინერგია განმეორებით ჩნდება. ეს ნიშნავს, რომ სისტემას აქვს დროის ისარი – მიმართულებით სიღრმეში ცვლილება.
თანდართული null‑ტესტები (ფაზების შერხევა, დროით გადაცვლა, სხვა წყვილებთან შედარება) გვაჩვენებს, რომ აღმოჩენილი ისარი მართლაც პროცესიდან მოდის და არა შემთხვევითი კონცხია.
სხვა სიტყვებით, ვეგას სისტემა გვეუბნება როგორ ვიპოვოთ და გავზომოთ ამ “ისრის” წარმოშობა რეალურ მონაცემებში. უბრალო „1,1,1“ ან „3,3,3“ ნომერაციის თქმა – ეს მხოლოდ სიმბოლოებია; ისინი არ გვაძლევს არც ფაზურ ურთიერთობას, არც სინერგიის რაოდენობრივ აღწერას და, მით უმეტეს, ვერ გვეუბნება, აქვს თუ არა სისტემას დროითი მიმართულება. ამ სისტრმით კი შესაძლებელია:
გაწერილი სიგნალებიდან გამოვლინდეს, როდის არიან ისინი სინქრონში;
რა პირობებში იბადება ახალი „სიღრმე“;
როგორ გავფილტროთ noise, რომ შედეგი არ იყოს არტეფაქტი.
ამიტომ კითხვაზე „აზრი?“ პასუხია: საჭირო არის, რათა მინიმალურ სახელდების ნაცვლად მივიღოთ მტკიცებულება – ნულოვან კონტროლებთან შედარებით გავიგოთ, არსებობს თუ არა პროცესში რეალური, ან არა შემთხვევითი, დროითი მიმართულება.
ტრიადული სისტემა, ანალიზი
თბილისის ფორუმი -> თემატური ფორუმი -> მეცნიერება და განათლება -> ტექნიკური და საბუნებისმეტყველო მეცნიერებები
