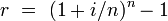ვერ დათვლი ეგრე შენი მიხვედრით, მაგისი ფორმულა არსებობს, სად მაქვს არ ვიცი, ზეპირად აღარ მახსოვს.
მოკლედ ესეთი რამეა, შენ რომ გიწერია წლიური პროცენტი გააჩნია იმას რა პერიოდულობით ფარავ, რაც უფრო მეტი გადახდა გიწევს ამ პერიოდის განმავლობაში რეითი მით მეტი გამოდის,
ანუ ეს არის რეალურად რამდენს იხდი.
შენ რო 21% გიწერია წლიური იმას ხო წელიწადში ერთხელ არ იხდი, ხოდა რაც უფრო მატულობს გადახდის პერიოდები ამ ერთი წლის განმავლობაში რეითი მით უფრო დიდია.
21-ზე გამოვიდა რო რეალურად რეითი იყო 23 თუ 24 პროცენტი, ეს ფინანსისტებში მიღებული ტერმნია და ძალიან კარგად იციან მისი "არსებობის" შესახებ, თუმცა, რა თქმა უნდა, მსესხებელს არ ეუბნებიან, რომ წლიური კი არის 21, მაგრამ ყოველთვიური გადახდის შედეგად ის რეალურად გამოდის 23.
* * *
The effective interest rate is calculated as if compounded annually. The effective rate is calculated in the following way, where r is the effective annual rate, i the nominal rate, and n the number of compounding periods per year (for example, 12 for monthly compounding):
For example, a nominal interest rate of 6% compounded monthly is equivalent to an effective interest rate of 6.17%. 6% compounded monthly is credited as 6%/12 = 0.005 every month. After one year, the initial capital is increased by the factor (1 + 0.005)12 ≈ 1.0617.
When the frequency of compounding is increased up to infinity the calculation will be:
The yield depends on the frequency of compounding:
Effective Annual Rate Based on Frequency of Compounding
Nominal Semi-Annual Quarterly Monthly Daily Continuous
1% 1.002% 1.004% 1.005% 1.005% 1.005%
5% 5.062% 5.095% 5.116% 5.127% 5.127%
10% 10.250% 10.381% 10.471% 10.516% 10.517%
15% 15.562% 15.865% 16.075% 16.180% 16.183%
20% 21.000% 21.551% 21.939% 22.134% 22.140%
30% 32.250% 33.547% 34.489% 34.969% 34.986%
40% 44.000% 46.410% 48.213% 49.150% 49.182%
50% 56.250% 60.181% 63.209% 64.816% 64.872%
This post has been edited by Fallen Angie on 2 Feb 2011, 21:02
მიმაგრებული სურათი
რამდენად გამჭვირვალეა საბანკო სექტორი საქართველოში, "0%-იანი სესხები" და ფარული საკომისიოები
