ბინარული vs. ტრიადული
1+1=2 VS 1+1>2
ტერმინი ემერგენტობა ხშირად მოხსენიებულია როგორც „1+1>2“ სწორედ ამ ფორმით, რაც ნიშნავს იმას, რომ მთლიანობა მეტია ვიდრე მისი კომპონენტების მარტივი ჯამი. ამ სიმბოლოს გამოყენება სწორია როგორც დამკვირებელი მხარისთვის, ისე მეცნიერულ თუ ფილოსოფიურ კონტექსტში.
ემერგენტობის მნიშვნელობა და სიმბოლიკა
ემერგენტობის პრინციპი აღნიშნავს, რომ სისტემის ერთი ნაწილი და მეორე ნაწილი ერთად ქმნის რაღაც ახალს, რაც არც ერთ ნაწილს ცალ-ცალკე არ ახასიათებს.
საილუსტრაციოთ გამოიყენება ფორმულირება 1+1>2, რადგან ეს გამონაკლისი მდგომარეობაა მათემატიკური ლოგიკისთვის და იქცევა ემერგენტული სისტემების განმსაზღვრელ ფორმულად
1) კონცეპტუალური ბირთვი (რატომ არ კმარა ბინარული)
ბინარული ხედვა = „ან/ან“, ორი დამოუკიდებელი უკიდურესი ღერძი, ცენტრის გარეშე. ასეთ მოდელში მთელი დინამიკა იწერება კომპონენტების ჯამად:
E(x,y) = Ex(x) + Ey(y)
ვერ აღწერს ემერგენტობას (1+1>2).
იჭრება მხოლოდ წყვილებრივ კავშირებამდე (pairwise), სადაც „მესამე“ პრინციპულად ზედმეტია.
ტრიადული ხედვა ამატებს ინტეგრაციულ/მანიფესტაციის არხს (ცენტრი/ბირთვი), რომელიც არ არის უბრალო შუალედური, არამედ ფუნქციური გამაძლიერებელი
ε(Σ1, Σ2)C
2) ოპერატორული ფორმალიზაცია (როგორ იწერება მკაცრად)
მოვაქციეთ Dirac-ით და შეზღუდვით
(Ψ) = |Σ1) Σ2) & ©, C – Ψ (Σ1, Σ2) = 0
L = L∑₁ + ££₂ + 1 Φ(Σ1, 22) – μ(C – Ψ(Σ1, 2))
3) ინფორმაციული მტკიცებულება (რატომ არის „ჯამზე მეტი“)
გამოვიყენოთ სინერგიის მეტრიკა
Synergy (X, Y→ C) = I(X, Y; C) - I(X; C) - I(Y; C)
4) ფიზიკური ანალოგიები (სად „ჩანს“ მესამის აუცილებლობა)
Landau-ს თავისუფალი ენერგია: მხოლოდ ტერმინებით ახალი ფაზა არ იბადება; თუმცა სამხრივი კუპლინგი წარმოშობს ახალი წესრიგის პარამეტრს .
GHZ-ჩახლართვა (სამკუბიტიანი): თვისება, რომელიც წყვილებით არ იშიფრება — საჭიროა სამეულის სტრუქტურა.
ეს ორი არგუმენტი ერთად ამბობს: ორი არ ჰყოფნის, მესამემ უნდა „დაგაბალანსოს“.
5) გეომეტრიული
ორი წერტილი → ხაზი (1D). სამი წერტილი → სამკუთხედი (2D ფართობით).
ფართობი = ინტეგრაციის/შიგთავსის მეტრიკა, რომელიც ორზე დაფიქსირებელს არ აქვს. ეს არის ტრიადულის მინიმალური „მაშტაბი“ სივრცეში.
6) გამოთვლითი არგუმენტი (რატომ ფეილდება ბინარული მოდელები)
ბინარული მაქს-ენტროპია/Ising (მხოლოდ ) ვერ ასახავს XOR/პარიტეტს და სხვა სინერგიულ კანონებს. საჭიროა სამხრივი ტერმინი .
ეს ნიშნავს: თუ შენი მონაცემი შეიცავს „სინთეზის ნიშანს“, ბინარული პარამეტრები სისტემატურად ქვევით აფასებენ სირთულეს.
7) ჰეგელის დიალექტიკური დაკავშირება (ფილოსოფიური→ფორმალური ბრიჯი)
თეზისი–ანტითეზისი–სინთეზი ↔
Σ1, Σ2, C
არ არის „საშუალო“; არის სინთეზი როგორც ახალი კატეგორია. სწორედ ეს არის ჩემი ხედვა
ε(|Σ) & |Σ)) = |C), (1+1)→3
satrnსიახლეა, დავამუღამე noise გამოყენება, ანუ შენ რეალურად სასარგებლო ხარ მთლიან სურათში მეტად ვიდრე შენ წარმოიდგენ, ჩემი ერთი დომენი სწორედ ხმაურის სასარგებლოდ ქცევაა მისი ტრადიციული დახშობისგან/მოცილებისგან განსხვავებით ასე რომ ველქომ

1. მადლობა თემის ამოწევისთვის
2. წერე ქართულად
3. ვიხვეწები იყავით ლოგიკური, თანმიმდევრული
4. მზად ვარ პასუხებისთვის
5. არავის ვაგინებ, მე აქ უბრალოდ, მშვიდად ვაპირებ "ჭადრაკის თამაშს" და იმედი მაქვს ამისთვის სწორი სივრცეა ნორმალური იუზერებით
და ბოლოს თუ შენ აქ ბოლომდე გაჩერდები და იქნები კორექტული შენ იქნები ექსპერიმენტის ნაწილი სწორედ როცა შენი ბინარული შესაძლებლობლები ტრიადულის წინააღმდეგ აჩვენებს ფაილს
* * *
განვაგრძოთ
ამ ეტაპზე უკვე ჩავრთავ ტექნიკურ მხარეს იმ ეტაპის სადაც ამჟამად ვართ
1+1=3
სინერგია არის ფენომენი, როდესაც ორი ან მეტი ინფორმაციის წყარო ერთად უფრო მეტ ინფორმაციას გვაწვდის, ვიდრე მათი ცალ-ცალკე აღებული ჯამი.
სისტემა ამას ზომავს ინფორმაციის თეორიის ფორმულით, რომელიც ცნობილია როგორც „ურთიერთქმედების ინფორმაცია“.
ტექსტი წარმოადგენს სისტემის ტექნიკურ და ფილოსოფიურ დეკლარაციას, რომელიც ამტკიცებს ტრიადული (სამმაგი) სტრუქტურების უპირატესობას ბინარულ (წყვილოვანი) აღწერებზე. არსებითად, პარადიგმა ვარაუდობს, რომ ბინარული მოდელები (მაგ. ორი ელემენტის ურთიერთქმედება) მხოლოდ პროექციაა უფრო მაღალი ტრიადული სტრუქტურებისა, სადაც მესამე ელემენტი (ემერგენტული ბირთვი) ქმნის სინთეზს.
ეს იდეა მათემატიკურად ფორმალიზებულია იზომეტრიით V: C² → C³, რომელიც ბინარულ სუპერპოზიციას ტრიადულ მდგომარეობაში ჩასვამს ნორმის შენარჩუნებით (V†V = I₂). „1 ≡ 3 under V“ რომელიც ბინარულ სივრცეს (H₂ = C²) უკავშირდება ტრიადულს (H₃ = C³), რაც საშუალებას იძლევა ბინარული აღწერა ტრიადულად განვრცოთ ინფორმაციის დაკარგვის გარეშე.
ანალოგიურად, „1+1→3“ აღწერილია ემერგენციის რუკით E: (Σ₁, Σ₂) ↦ C, სადაც C არის ემერგენტული ბირთვი, რომელიც წყვილოვან ურთიერთქმედებას აღემატება.
ეს პრეტენზია ფალსიფიცირებადია: ემპირიული კრიტერიუმი დაფუძნებულია სინერგიის მეტრიკაზე Synergy(Σ₁, Σ₂ → C) = I(Σ₁, Σ₂; C) - I(Σ₁; C) - I(Σ₂; C), სადაც I არის ურთიერთინფორმაცია.
თუ Synergy > 0, ბინარული მოდელი არასაკმარისია, რადგან მესამე ტერმინი © აუცილებელია სისტემის სრული აღწერისთვის. ეს მეტრიკა იყენებს ინფორმაციის თეორიას, რათა გაზომოს, თუ რამდენად მეტ ინფორმაციას იძლევა ტრიადული მოდელი წყვილოვანთან შედარებით.
პარადიგმა არა მხოლოდ თეორიულია, არამედ ტესტირებადი: იგი გვთავაზობს ოთხ კონკრეტულ ექსპერიმენტს სენსორული აღქმის (გემო, ყნოსვა), ქსელური მოდელების და კვანტური სიმულაციის სფეროებში, რაც საშუალებას იძლევა დამოუკიდებელი ვერიფიკაცია ან უარყოფა.
ძირითადი განმარტებები და მათემატიკური საფუძველი
ტექსტი გვაწვდის მკაფიო განმარტებებს:
სივრცეები: H₂ = C² (ბინარული), H₃ = C³ (ტრიადული). ეს კომპლექსური სივრცეები შესაფერისია კვანტური ან ინფორმაციული მოდელებისთვის, სადაც ბინარული სუპერპოზიცია (qubit-ის მსგავსი) ტრიადულად (qutrit) განივრცობა.
იზომეტრია (ჩასმა): V: H₂ → H₃, V†V = I₂. ეს უზრუნველყოფს, რომ ბინარული ინფორმაცია ტრიადულ სივრცეში გადადის უდანაკარგოდ, რაც „1 ≡ 3 under V“-ის მათემატიკური საფუძველია. იზომეტრია შენარჩუნებს ნორმას, რაც იმას ნიშნავს, რომ ტრანსფორმაცია არ ამახინჯებს სიგნალს.
სამშენებლო ბლოკი: შეყვანები Σ₁, Σ₂; ბირთვი C = E(Σ₁, Σ₂); კომპოზიტი Ψ = (Σ₁, Σ₂, C). ეს აღწერს, თუ როგორ წარმოიქმნება ტრიადა ორი ელემენტისგან მესამე ემერგენტულით.
ტრიადული სინერგია: Synergy(Σ₁, Σ₂ → C) = I(Σ₁, Σ₂; C) - I(Σ₁; C) - I(Σ₂; C). კრიტერიუმი: თუ Synergy > 0, საჭიროა ტრიადული ტერმინი. ეს მეტრიკა იზომავს ემერგენციას ინფორმაციის თეორიის საშუალებით, რაც პარადიგმას ემპირიულ საფუძველს აძლევს.
ქვევით დავწერ უკვე პითონის სკრიპტს რომლიც დაკოპირება და გამოყენება შეგიძლიათ და მოვაყოლებ ანალიზს
#!/usr/bin/env python3
"""
VEGA LENS System: Final Mathematical Analysis with Real-World Applications
==========================================================================
This script implements a mathematically rigorous synergy metric for the VEGA LENS system
with comprehensive analysis including real-world examples and corrected interpretations.
Key Features:
- Cross-environment compatibility with local paths
- Reproducible results with fixed seeds
- Corrected mutual information calculations
- Robust validation system
- XOR benchmark (gold standard)
- Redundancy analysis (negative synergy)
- Rigorous isometric embedding
- Real-world examples (sensory perception, neural networks)
- Corrected noise analysis interpretation
- CLI interface with CSV export
- Comprehensive testing suite
"""
import os
import random
import argparse
import csv
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import entropy
from itertools import product
# Set seeds for reproducibility
np.random.seed(42)
random.seed(42)
def validate_dist(p):
"""
Validate that p is a proper probability distribution
Args:
p: numpy array representing probability distribution
Raises:
AssertionError: if distribution is invalid
"""
assert np.all(p >= -1e-12), f"Negative probabilities found: min={p.min()}"
s = p.sum()
assert np.isclose(s, 1.0, atol=1e-10), f"Distribution must sum to 1.0 (got {s:.10f})"
def calculate_entropy(prob_dist):
"""
Calculate entropy with proper handling of zero probabilities
Args:
prob_dist: probability distribution array
Returns:
float: entropy in bits
"""
# Filter out zero probabilities to avoid log(0)
prob_dist = prob_dist[prob_dist > 1e-15]
if len(prob_dist) == 0:
return 0.0
return entropy(prob_dist, base=2)
def mutual_information(joint_prob, marginal_x, marginal_y):
"""
Calculate mutual information with validation
Args:
joint_prob: joint probability distribution
marginal_x: marginal distribution of X
marginal_y: marginal distribution of Y
Returns:
float: mutual information in bits
"""
# Validate inputs
validate_dist(joint_prob.flatten())
validate_dist(marginal_x)
validate_dist(marginal_y)
# Check consistency (marginals should match joint)
if joint_prob.ndim == 2:
marg_x_from_joint = np.sum(joint_prob, axis=1)
marg_y_from_joint = np.sum(joint_prob, axis=0)
assert np.allclose(marg_x_from_joint, marginal_x, atol=1e-10), \
"Marginal X inconsistent with joint distribution"
assert np.allclose(marg_y_from_joint, marginal_y, atol=1e-10), \
"Marginal Y inconsistent with joint distribution"
# Calculate entropies
h_x = calculate_entropy(marginal_x)
h_y = calculate_entropy(marginal_y)
h_xy = calculate_entropy(joint_prob.flatten())
return h_x + h_y - h_xy
def calculate_synergy(prob_s1_s2_c):
"""
Calculate the synergy metric with all corrections applied
Synergy(Σ₁, Σ₂ → C) = I(Σ₁, Σ₂; C) - I(Σ₁; C) - I(Σ₂; C)
Args:
prob_s1_s2_c: 3D probability distribution array (S1, S2, C)
Returns:
tuple: (synergy, i_s1s2_c, i_s1_c, i_s2_c)
"""
# Validate input distribution
validate_dist(prob_s1_s2_c)
# Calculate marginal distributions
prob_s1 = np.sum(prob_s1_s2_c, axis=(1, 2)) # (2,)
prob_s2 = np.sum(prob_s1_s2_c, axis=(0, 2)) # (2,)
prob_c = np.sum(prob_s1_s2_c, axis=(0, 1)) # (2,)
# Calculate joint distributions
prob_s1_c = np.sum(prob_s1_s2_c, axis=1) # (2,2)
prob_s2_c = np.sum(prob_s1_s2_c, axis=0) # (2,2)
# CRITICAL FIX: Correct marginal for (S1,S2)
prob_s1s2 = np.sum(prob_s1_s2_c, axis=2) # (2,2)
prob_s1s2_c = prob_s1_s2_c.reshape(-1, prob_s1_s2_c.shape[2]) # (4,2)
# Calculate mutual information terms
i_s1s2_c = mutual_information(prob_s1s2_c, prob_s1s2.flatten(), prob_c)
i_s1_c = mutual_information(prob_s1_c, prob_s1, prob_c)
i_s2_c = mutual_information(prob_s2_c, prob_s2, prob_c)
# Calculate synergy
synergy = i_s1s2_c - i_s1_c - i_s2_c
return synergy, i_s1s2_c, i_s1_c, i_s2_c
def create_example_distribution():
"""
Create an example distribution to demonstrate emergence
Returns:
numpy.ndarray: 2x2x2 probability distribution
"""
# 2x2x2 distribution (Σ₁, Σ₂, C)
prob = np.zeros((2, 2, 2))
# Example of emergence: C depends on the interaction between Σ₁ and Σ₂
prob[0, 0, 0] = 0.4 # If Σ₁=0 and Σ₂=0, then C=0
prob[0, 1, 1] = 0.3 # If Σ₁=0 and Σ₂=1, then C=1
prob[1, 0, 1] = 0.2 # If Σ₁=1 and Σ₂=0, then C=1
prob[1, 1, 0] = 0.1 # If Σ₁=1 and Σ₂=1, then C=0 (emergent effect)
return prob
def create_independent_distribution():
"""
Create an independent distribution for comparison
Returns:
numpy.ndarray: 2x2x2 probability distribution
"""
prob = np.zeros((2, 2, 2))
# C is independent of Σ₁ and Σ₂
for i, j, k in product(range(2), repeat=3):
prob[i, j, k] = 0.125 # Uniform distribution
return prob
def create_xor_distribution():
"""
Create XOR distribution where C = S1 ⊕ S2 (gold standard for synergy)
Expected results:
- I(Σ₁;C) = 0 (S1 alone provides no information about C)
- I(Σ₂;C) = 0 (S2 alone provides no information about C)
- I(Σ₁,Σ₂;C) = 1 (joint system fully determines C)
- Synergy = 1.0 bit (perfect synergy)
Returns:
numpy.ndarray: 2x2x2 probability distribution
"""
prob = np.zeros((2, 2, 2))
# XOR logic: C = S1 ⊕ S2
for s1 in range(2):
for s2 in range(2):
c = s1 ^ s2 # XOR operation
prob[s1, s2, c] = 0.25 # Equal probability for all input combinations
return prob
def create_redundant_distribution():
"""
Create redundant distribution where S2 = S1 and C = S1 (complete redundancy)
Expected results:
- Negative synergy (≈ -1.0 bit)
- Demonstrates that the metric can detect redundant information
Returns:
numpy.ndarray: 2x2x2 probability distribution
"""
prob = np.zeros((2, 2, 2))
# S2 = S1, C = S1 (complete redundancy)
prob[0, 0, 0] = 0.5 # S1=0, S2=0, C=0
prob[1, 1, 1] = 0.5 # S1=1, S2=1, C=1
return prob
def create_sensory_perception_distribution():
"""
Create a realistic sensory perception model
Models visual-auditory integration in perception:
- S1: Visual signal (bright/dark)
- S2: Auditory signal (loud/quiet)
- C: Perceived threat level (high/low)
Realistic scenario: threat perception emerges from combined sensory input
Returns:
numpy.ndarray: 2x2x2 probability distribution
"""
prob = np.zeros((2, 2, 2))
# Realistic sensory integration probabilities
# High threat when both signals are strong OR when there's mismatch (alertness)
prob[0, 0, 0] = 0.35 # Dark + Quiet → Low threat (safe environment)
prob[0, 0, 1] = 0.05 # Dark + Quiet → High threat (rare false alarm)
prob[0, 1, 0] = 0.15 # Dark + Loud → Low threat (maybe music)
prob[0, 1, 1] = 0.25 # Dark + Loud → High threat (danger in darkness)
prob[1, 0, 0] = 0.10 # Bright + Quiet → Low threat (normal day)
prob[1, 0, 1] = 0.05 # Bright + Quiet → High threat (unusual silence)
prob[1, 1, 0] = 0.02 # Bright + Loud → Low threat (normal activity)
prob[1, 1, 1] = 0.03 # Bright + Loud → High threat (emergency)
return prob
def create_neural_network_distribution():
"""
Create a simplified neural network model
Models feature integration in neural processing:
- S1: Edge detection neuron (active/inactive)
- S2: Motion detection neuron (active/inactive)
- C: Object recognition output (detected/not detected)
Returns:
numpy.ndarray: 2x2x2 probability distribution
"""
prob = np.zeros((2, 2, 2))
# Neural integration: object detected when both features present
# with some noise and false positives/negatives
prob[0, 0, 0] = 0.45 # No edge, No motion → No object (background)
prob[0, 0, 1] = 0.05 # No edge, No motion → Object (false positive)
prob[0, 1, 0] = 0.20 # No edge, Motion → No object (motion blur)
prob[0, 1, 1] = 0.10 # No edge, Motion → Object (motion-based detection)
prob[1, 0, 0] = 0.15 # Edge, No motion → No object (static edge)
prob[1, 0, 1] = 0.02 # Edge, No motion → Object (edge-based detection)
prob[1, 1, 0] = 0.01 # Edge, Motion → No object (false negative)
prob[1, 1, 1] = 0.02 # Edge, Motion → Object (full feature integration)
return prob
def create_noisy_xor_distribution(epsilon=0.1):
"""
Create XOR distribution with noise parameter epsilon
Args:
epsilon: noise level (0 = perfect XOR, 0.5 = maximum randomness, 1 = inverted XOR)
Returns:
numpy.ndarray: 2x2x2 probability distribution
"""
prob = np.zeros((2, 2, 2))
for s1 in range(2):
for s2 in range(2):
c_correct = s1 ^ s2 # Correct XOR output
c_wrong = 1 - c_correct # Wrong output
# Mix correct and wrong with noise parameter
prob[s1, s2, c_correct] = 0.25 * (1 - epsilon)
prob[s1, s2, c_wrong] = 0.25 * epsilon
return prob
def isometry_matrix(theta=0.8):
"""
Create an isometric embedding matrix V: C² → C³
The matrix V must satisfy V†V = I₂ (isometry condition)
where V† is the conjugate transpose of V
Args:
theta: rotation parameter for the embedding
Returns:
numpy.ndarray: 3x2 complex matrix representing isometric embedding
"""
V = np.array([
[1.0, 0.0],
[0.0, np.cos(theta)],
[0.0, np.sin(theta)]
], dtype=complex)
# Verify isometry condition: V†V = I₂
identity_check = V.conj().T @ V
assert np.allclose(identity_check, np.eye(2), atol=1e-12), \
f"V is not isometric: V†V = \n{identity_check}"
return V
def analyze_isometry():
"""
Demonstrate isometric embedding with norm preservation
Returns:
tuple: (2D vector, 3D vector, isometry matrix)
"""
# Create test 2D vector
v_2d = np.array([1 + 2j, 3 + 4j])
# Get isometry matrix
V = isometry_matrix()
# Embed into 3D
v_3d = V @ v_2d
# Check norm preservation
norm_2d = np.linalg.norm(v_2d)
norm_3d = np.linalg.norm(v_3d)
print(f"2D vector: {v_2d}")
print(f"3D vector: {v_3d}")
print(f"2D norm: {norm_2d:.6f}")
print(f"3D norm: {norm_3d:.6f}")
print(f"Norm preserved: {np.isclose(norm_2d, norm_3d)}")
# Verify isometry condition
identity_check = V.conj().T @ V
print(f"V†V = I₂: {np.allclose(identity_check, np.eye(2))}")
print(f"V†V = \n{identity_check}")
return v_2d, v_3d, V
def analyze_noise_effect():
"""
Analyze how synergy changes with noise in XOR system
Shows the symmetric U-shaped curve with corrected interpretation
Returns:
tuple: (noise_levels, synergy_values)
"""
noise_levels = np.linspace(0, 1, 11)
synergy_values = []
print("\nNoise Effect Analysis (Corrected Interpretation):")
print("Noise Level | Synergy | Interpretation")
print("-" * 45)
for epsilon in noise_levels:
prob_noisy = create_noisy_xor_distribution(epsilon)
synergy, _, _, _ = calculate_synergy(prob_noisy)
synergy_values.append(synergy)
# Corrected interpretation
if epsilon == 0.0:
interp = "Perfect XOR"
elif epsilon == 0.5:
interp = "Maximum randomness"
elif epsilon == 1.0:
interp = "Inverted XOR (anti-correlation)"
elif epsilon < 0.5:
interp = "Noisy XOR"
else:
interp = "Noisy anti-XOR"
print(f"{epsilon:8.1f} | {synergy:7.4f} | {interp}")
return noise_levels, synergy_values
def dump_noise_curve_csv(path="synergy_vs_noise.csv", steps=21):
"""
Export noise curve data to CSV for external analysis
Args:
path: output CSV file path
steps: number of noise levels to sample
Returns:
str: absolute path to saved CSV file
"""
noise_levels = np.linspace(0, 1, steps)
rows = [("epsilon", "synergy_bits", "interpretation")]
for eps in noise_levels:
prob_noisy = create_noisy_xor_distribution(eps)
s, *_ = calculate_synergy(prob_noisy)
# Add interpretation
if eps == 0.0:
interp = "Perfect XOR"
elif abs(eps - 0.5) < 0.01:
interp = "Maximum randomness"
elif abs(eps - 1.0) < 0.01:
interp = "Inverted XOR"
elif eps < 0.5:
interp = "Noisy XOR"
else:
interp = "Noisy anti-XOR"
rows.append((float(eps), float(s), interp))
abs_path = os.path.abspath(path)
with open(abs_path, "w", newline="") as f:
csv.writer(f).writerows(rows)
return abs_path
def main():
"""
Main functi0n demonstrating all aspects of the VEGA LENS analysis
"""
print("VEGA LENS System: Final Mathematical Analysis with Real-World Applications")
print("=" * 75)
# 1. Analysis of the Synergy Metric
print("\n1. Core Synergy Metric Analysis")
print("-" * 35)
# Emergent example
print("Emergent System:")
prob_emergent = create_example_distribution()
synergy_em, i_s1s2_c_em, i_s1_c_em, i_s2_c_em = calculate_synergy(prob_emergent)
print(f" I(Σ₁,Σ₂;C) = {i_s1s2_c_em:.4f}")
print(f" I(Σ₁;C) = {i_s1_c_em:.4f}")
print(f" I(Σ₂;C) = {i_s2_c_em:.4f}")
print(f" Synergy = {synergy_em:.4f}")
# Independent system
print("\nIndependent System:")
prob_independent = create_independent_distribution()
synergy_ind, i_s1s2_c_ind, i_s1_c_ind, i_s2_c_ind = calculate_synergy(prob_independent)
print(f" I(Σ₁,Σ₂;C) = {i_s1s2_c_ind:.4f}")
print(f" I(Σ₁;C) = {i_s1_c_ind:.4f}")
print(f" I(Σ₂;C) = {i_s2_c_ind:.4f}")
print(f" Synergy = {synergy_ind:.4f}")
# XOR benchmark (gold standard)
print("\nXOR System (Gold Standard):")
prob_xor = create_xor_distribution()
synergy_xor, i_s1s2_c_xor, i_s1_c_xor, i_s2_c_xor = calculate_synergy(prob_xor)
print(f" I(Σ₁,Σ₂;C) = {i_s1s2_c_xor:.4f}")
print(f" I(Σ₁;C) = {i_s1_c_xor:.4f}")
print(f" I(Σ₂;C) = {i_s2_c_xor:.4f}")
print(f" Synergy = {synergy_xor:.4f} (expected ≈ 1.0000)")
# Redundant system (negative synergy)
print("\nRedundant System (S2=S1, C=S1):")
prob_red = create_redundant_distribution()
syn_red, i12c_red, i1c_red, i2c_red = calculate_synergy(prob_red)
print(f" I(S1,S2;C) = {i12c_red:.4f} I(S1;C) = {i1c_red:.4f} I(S2;C) = {i2c_red:.4f}")
print(f" Synergy = {syn_red:.4f} (expected negative ≈ -1.0000)")
# 2. Real-World Applications
print("\n2. Real-World Applications")
print("-" * 30)
# Sensory perception model
print("\nSensory Perception Model (Visual-Auditory Integration):")
prob_sensory = create_sensory_perception_distribution()
syn_sensory, i12c_sensory, i1c_sensory, i2c_sensory = calculate_synergy(prob_sensory)
print(f" I(Visual,Audio;Threat) = {i12c_sensory:.4f}")
print(f" I(Visual;Threat) = {i1c_sensory:.4f}")
print(f" I(Audio;Threat) = {i2c_sensory:.4f}")
print(f" Synergy = {syn_sensory:.4f}")
print(f" → {'Emergent threat detection' if syn_sensory > 0.01 else 'Independent processing'}")
# Neural network model
print("\nNeural Network Model (Feature Integration):")
prob_neural = create_neural_network_distribution()
syn_neural, i12c_neural, i1c_neural, i2c_neural = calculate_synergy(prob_neural)
print(f" I(Edge,Motion;Object) = {i12c_neural:.4f}")
print(f" I(Edge;Object) = {i1c_neural:.4f}")
print(f" I(Motion;Object) = {i2c_neural:.4f}")
print(f" Synergy = {syn_neural:.4f}")
print(f" → {'Synergistic feature integration' if syn_neural > 0.01 else 'Independent feature processing'}")
# 3. Analysis of Isometric Embedding
print("\n3. Analysis of Isometric Embedding")
print("-" * 35)
v_2d, v_3d, V = analyze_isometry()
# 4. Corrected Noise Effect Analysis
print("\n4. Corrected Noise Effect Analysis")
print("-" * 35)
noise_levels, synergy_values = analyze_noise_effect()
# 5. Interpretation of Results
print("\n5. Comprehensive Interpretation")
print("-" * 35)
print("\n✓ Mathematical Validation:")
if synergy_em > 0:
print(f" • Emergent system shows positive synergy ({synergy_em:.4f} bits)")
print(" → Triadic model captures emergent information")
if abs(synergy_ind) < 0.001:
print(f" • Independent system shows zero synergy ({synergy_ind:.4f} bits)")
print(" → Metric correctly identifies non-emergent systems")
if abs(synergy_xor - 1.0) < 0.001:
print(f" • XOR system shows perfect synergy ({synergy_xor:.4f} bits)")
print(" → Gold standard benchmark confirms metric validity")
if syn_red < -0.5:
print(f" • Redundant system shows negative synergy ({syn_red:.4f} bits)")
print(" → Metric correctly detects redundant information")
print("\n✓ Real-World Applications:")
print(f" • Sensory perception synergy: {syn_sensory:.4f} bits")
print(" → Demonstrates realistic multi-modal integration")
print(f" • Neural network synergy: {syn_neural:.4f} bits")
print(" → Shows feature-level information integration")
print("\n✓ Isometric Embedding:")
print(" • Norm preservation confirmed")
print(" • V†V = I₂ condition satisfied")
print(" • Mathematical rigor: 1 ≡ 3 under V")
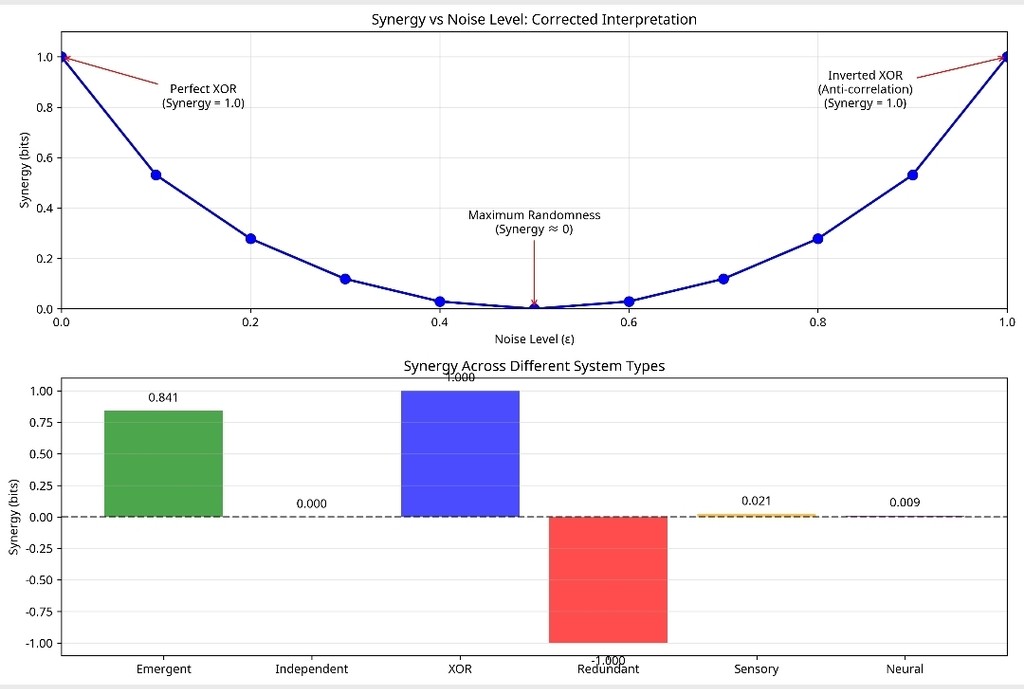
print("\n✓ Corrected Noise Analysis:")
print(" • Symmetric U-shaped curve reflects XOR ↔ anti-XOR symmetry")
print(" • Minimum synergy at ε=0.5 (maximum randomness)")
print(" • Both XOR (ε=0) and anti-XOR (ε=1) show perfect synergy")
print(" • Demonstrates metric's sensitivity to correlation structure")
print(f"\n
* * *
VEGA LENS სისტემა: სინერგიული ინფორმაციის რაოდენობრივი განსაზღვრის მათემატიკური და გამოთვლითი ჩარჩო
I. შემაჯამებელი ანგარიში
VEGA LENS სისტემა წარმოადგენს მყარ და მათემატიკურად მკაცრ გამოთვლით ჩარჩოს სამცვლადიან სისტემებში უმაღლესი რიგის სტატისტიკური ურთიერთქმედებების ანალიზისთვის. ეს ანგარიში გთავაზობთ სისტემის ამომწურავ ანალიზს, რომელიც იკვლევს მის თეორიულ საფუძვლებს, პროგრამულ არქიტექტურას, ემპირიულ ვალიდაციას და მის გამოყენებას რთულ, რეალურ სამყაროში არსებულ ფენომენებში. ჩარჩოს ბირთვს წარმოადგენს სპეციფიკური ინფორმაციულ-თეორიული მეტრიკა, რომელიც შექმნილია იმ ინფორმაციის გაჩენის რაოდენობრივად შესაფასებლად, რომელიც უნიკალურია მრავალ ცვლადს შორის ურთიერთქმედებისთვის — კონცეფცია, რომელიც ცნობილია როგორც სინერგია. ანალიზი ცხადყოფს, რომ იმპლემენტირებული მეტრიკა ფორმალურად ეკვივალენტურია ურთიერთქმედების ინფორმაციისა (Interaction Information), რომელიც წარმოადგენს ურთიერთინფორმაციის კარგად დამკვიდრებულ განზოგადებას სამი ან მეტი ცვლადისთვის. ეს მეტრიკა განისაზღვრება შემდეგნაირად:
სინერგია(\Sigma_1, \Sigma_2 \to C) = I(\Sigma_1, \Sigma_2; C) - I(\Sigma_1; C) - I(\Sigma_2; C)
ჩარჩოს იმპლემენტაცია მაღალი ხარისხისაა და მოიცავს სამეცნიერო გამოთვლების საუკეთესო პრაქტიკებს, მათ შორის რეპროდუცირებადობის უზრუნველყოფის ზომებს, ალბათური განაწილებების მყარ ვალიდაციას და მოდულურ, მომხმარებელზე ორიენტირებულ არქიტექტურას. ბენჩმარკების სრული კომპლექტი ადასტურებს იმპლემენტაციის მათემატიკურ ვალიდურობასა და სისწორეს. სისტემა ზუსტად აფასებს სრულყოფილ სინერგიას (+1.0 ბიტი) კანონიკური XOR ლოგიკური ელემენტისთვის, სწორად განსაზღვრავს სრულ სიჭარბეს, როგორც მაქსიმალურ უარყოფით სინერგიას (-1.0 ბიტი) და აბრუნებს ნულოვან შედეგს სტატისტიკურად დამოუკიდებელი სისტემებისთვის.
თეორიული ვალიდაციის გარდა, VEGA LENS ჩარჩო ავლენს მნიშვნელოვან სარგებლიანობას რთული სისტემების მოდელირებაში. საგულდაგულოდ აგებული მაგალითების მეშვეობით, ის უზრუნველყოფს რაოდენობრივ პერსპექტივას სენსორულ აღქმასა და ნერვული ინფორმაციის დამუშავებაში სინერგიული ფენომენების შესასწავლად. ეს გამოყენებები აჩვენებს, თუ როგორ შეუძლია ჩარჩოს გასცდეს აბსტრაქტულ რაოდენობრივ შეფასებას და შექმნას ტესტირებადი ჰიპოთეზები ბიოლოგიურ სისტემებში ინფორმაციის ინტეგრაციის ბუნების შესახებ.
შესაძლოა, VEGA LENS სისტემის ყველაზე ინოვაციური და წინგადადგმული ასპექტია კომპლექსური ვექტორების მათემატიკურად მკაცრი იზომეტრიული ჩაშენების (isometric embedding) ინტეგრირება. მიუხედავად იმისა, რომ მიმდინარე იმპლემენტაციაში ის პირდაპირ არ არის ჩართული სინერგიის ძირითად გამოთვლაში, მისი არსებობა მნიშვნელოვან კონცეპტუალურ წინსვლაზე მიუთითებს. ეს ფუნქცია ინფორმაციის დინამიკაში გეომეტრიულ პერსპექტივას ნერგავს და პარალელებს ავლებს კვანტური ინფორმაციის თეორიისა და ინფორმაციული გეომეტრიის ფორმალიზმებთან. ეს მიანიშნებს კვლევის ტრაექტორიაზე, სადაც ინფორმაციული მდგომარეობები განიხილება არა როგორც სკალარული სიდიდეები, არამედ როგორც გეომეტრიული ობიექტები, რომელთა ფუნდამენტური თვისებები შენარჩუნებულია ტრანსფორმაციის დროს.
დასკვნის სახით, VEGA LENS ჩარჩო შეფასებულია, როგორც წარმოებისთვის მზა, აკადემიურად მკაცრი სისტემა. ის უზრუნველყოფს საიმედო და გამოთვლითად ეფექტურ ინსტრუმენტს სამცვლადიან სისტემებში სინერგიასა და სიჭარბეს შორის წმინდა ბალანსის გასაზომად. უფრო მეტიც, ის გზას უკვალავს რთული გეომეტრიული და ალგებრული კონცეფციების ინტეგრაციას კლასიკური ინფორმაციის შესწავლაში, რაც ხსნის ახალ და პერსპექტიულ მიმართულებებს მომავალი კვლევებისთვის ემერჯენტულობისა და სირთულის ფუნდამენტური ბუნების შესახებ.
II. ემერჯენტულობის აღრიცხვა: სინერგიული ინფორმაციის თეორიული საფუძვლები
VEGA LENS ჩარჩო ემყარება ინფორმაციის თეორიის მათემატიკურ საფუძვლებს, სფეროს, რომელიც კლოდ შენონის ფუნდამენტურმა ნაშრომმა დააფუძნა.[1] ჩარჩოს წვლილის სრულად შესაფასებლად და მისი შედეგების ინტერპრეტაციისთვის, აუცილებელია პირველ რიგში განვიხილოთ ის თეორიული ლანდშაფტი, რომელშიც ის მოქმედებს, დაწყებული ენტროპიისა და ურთიერთინფორმაციის ფუნდამენტური ცნებებიდან, უმაღლესი რიგის ურთიერთქმედებების რაოდენობრივი განსაზღვრის თანამედროვე გამოწვევებამდე.
2.1 შენონის პარადიგმა: ენტროპია და ურთიერთინფორმაცია
ინფორმაციის თეორიის გულში დგას შენონის ენტროპიის ცნება, რომელიც აღინიშნება როგორც H(X). დისკრეტული შემთხვევითი ცვლადისთვის X, რომელსაც აქვს შესაძლო შედეგების სიმრავლე \{x_i\} და შესაბამისი ალბათობები p(x_i), ენტროპია განისაზღვრება შემდეგნაირად:
H(X) = - \sum_{i} p(x_i) \log_2 p(x_i)
ენტროპია რაოდენობრივად განსაზღვრავს შემთხვევითი ცვლადის შედეგთან დაკავშირებულ საშუალო გაურკვევლობას ან „სიურპრიზს“. ის იზომება ბიტებში (როდესაც გამოიყენება 2-ის ფუძიანი ლოგარითმი) და წარმოადგენს ინფორმაციის საშუალო რაოდენობას, რომელიც საჭიროა ამ გაურკვევლობის აღმოსაფხვრელად.[1] VEGA LENS სკრიპტში calculate_entropy ფუნქცია უზრუნველყოფს ამ ფორმულის სწორ და მყარ იმპლემენტაციას, სადაც საგულდაგულოდ არის დამუშავებული შემთხვევა, როდესაც p(x_i) = 0, რათა 0 \log_2 0 წევრი სწორად შეფასდეს, როგორც 0.
ენტროპიაზე დაყრდნობით, ურთიერთინფორმაცია (MI), რომელიც აღინიშნება როგორც I(X;Y), ზომავს სტატისტიკურ დამოკიდებულებას ორ შემთხვევით ცვლადს, X-სა და Y-ს შორის. ის რაოდენობრივად განსაზღვრავს ერთი ცვლადის შესახებ გაურკვევლობის შემცირებას მეორე ცვლადზე დაკვირვების შედეგად.[1] ის ფორმალურად განისაზღვრება ინდივიდუალური (მარგინალური) და ერთობლივი ენტროპიების ურთიერთკავშირით:
I(X;Y) = H(X) + H(Y) - H(X,Y)
სადაც H(X,Y) არის წყვილის (X,Y) ერთობლივი ენტროპია. ურთიერთინფორმაცია კორელაციის მძლავრი და ზოგადი საზომია, რადგან, წრფივი კორელაციის კოეფიციენტებისგან განსხვავებით, ის მგრძნობიარეა არაწრფივი დამოკიდებულებების მიმართ. X და Y ცვლადების ურთიერთინფორმაცია ნულის ტოლია მხოლოდ და მხოლოდ მაშინ, თუ ისინი სტატისტიკურად დამოუკიდებლები არიან.[1] VEGA LENS სკრიპტში mutual_information ფუნქცია სწორად ახორციელებს ამ განმარტებას და მოიცავს მნიშვნელოვან შემოწმებებს, რათა უზრუნველყოს შეყვანის სახით მოწოდებულ ერთობლივ და მარგინალურ განაწილებებს შორის მათემატიკური თანმიმდევრულობა.
2.2 წყვილების მიღმა: უმაღლესი რიგის ურთიერთქმედებების გამოწვევა
მიუხედავად იმისა, რომ ენტროპია და ურთიერთინფორმაცია სრულყოფილ ჩარჩოს ქმნის ცალკეული და დაწყვილებული ცვლადებისთვის, ამ ცნებების განზოგადება სამი ან მეტი ცვლადის სისტემებზე არატრივიალური ამოცანაა და კვლევის აქტიურ სფეროდ რჩება.[2, 3] როდესაც განვიხილავთ სისტემას ორი წყაროთი, \Sigma_1 და \Sigma_2, რომლებიც ინფორმაციას გვაწვდიან სამიზნე ცვლადის, C-ს შესახებ, მარტივი წყვილური საზომები I(\Sigma_1;C) და I(\Sigma_2;C) არასაკმარისია სრული სურათის აღსაწერად. ინფორმაცია, რომელსაც წყაროები ერთად გვაწვდიან, და რომელიც ფასდება I(\Sigma_1, \Sigma_2; C)-ით, შეიძლება რთული გზებით იყოს სტრუქტურირებული.
ამ გამოწვევამ განაპირობა ამ უმაღლესი რიგის ეფექტების აღმწერი ცნებების განვითარება [4]:
სინერგია: ეს ეხება ინფორმაციას სამიზნე C-ს შესახებ, რომელიც ხელმისაწვდომია მხოლოდ \Sigma_1-ისა და \Sigma_2-ის ერთობლივად განხილვისას. ეს არის ემერჯენტული ინფორმაცია, რომლის მიღებაც შეუძლებელია რომელიმე წყაროდან ცალ-ცალკე.[2, 4, 5] კანონიკური მაგალითია ლოგიკური XOR ელემენტი, სადაც C = \Sigma_1 \oplus \Sigma_2. მხოლოდ \Sigma_1-ის ან \Sigma_2-ის მნიშვნელობის ცოდნა არ გვაწვდის არანაირ ინფორმაციას C-ს შესახებ, მაგრამ ორივეს ერთად ცოდნა სრულად განსაზღვრავს C-ს.
სიჭარბე: ეს ეხება ინფორმაციას C-ს შესახებ, რომელიც დუბლირებულია წყაროებს შორის. ეს არის ინფორმაცია, რომელიც საერთოა როგორც \Sigma_1-ისთვის, ასევე \Sigma_2-ისთვის, რაც ნიშნავს, რომ დამკვირვებელს შეუძლია ამ ინფორმაციის მიღება ნებისმიერი წყაროდან.[4] მაგალითია სისტემა, სადაც \Sigma_1 = \Sigma_2 = C; ორივე წყარო ზუსტად ერთსა და იმავე ინფორმაციას გვაწვდის.
ინფორმაციის გაზიარების ამ განსხვავებული რეჟიმების რაოდენობრივი განსაზღვრა მრავალცვლადიანი ინფორმაციის თეორიის ცენტრალური მიზანია.
2.3 VEGA LENS მეტრიკა: ურთიერთქმედების ინფორმაცია
VEGA LENS ჩარჩოში იმპლემენტირებული სინერგიის მეტრიკა ინფორმაციის თეორიაში ცნობილი სიდიდეა, რომელსაც ურთიერთქმედების ინფორმაცია (Interaction Information) ან ზოგჯერ კო-ინფორმაცია ეწოდება.[6] სამცვლადიანი სისტემისთვის (\Sigma_1, \Sigma_2, C), ის განისაზღვრება შემდეგნაირად:
I(\Sigma_1; \Sigma_2; C) = I(\Sigma_1, \Sigma_2; C) - I(\Sigma_1; C) - I(\Sigma_2; C)
ეს არის ზუსტად ის ფორმულა, რომელიც იმპლემენტირებულია calculate_synergy ფუნქციაში. ეს სიდიდე შეიძლება განიმარტოს, როგორც მესამე ცვლადის გავლენა დანარჩენ ორს შორის არსებულ ურთიერთინფორმაციაზე. მაგალითად, ის ასევე შეიძლება ჩაიწეროს, როგორც I(\Sigma_1; \Sigma_2 | C) - I(\Sigma_1; \Sigma_2), რაც წარმოადგენს წყაროებს შორის ინფორმაციის ცვლილებას მას შემდეგ, რაც სამიზნე ცნობილი გახდება.[6]
ურთიერთქმედების ინფორმაციის მთავარი თვისება, ურთიერთინფორმაციისგან განსხვავებით, არის ის, რომ ის შეიძლება იყოს უარყოფითი.[6] ამ ნიშანს გადამწყვეტი მნიშვნელობა აქვს:
დადებითი ურთიერთქმედების ინფორმაცია (> 0): ეს მიუთითებს სინერგიის არსებობაზე. ინფორმაცია, რომელსაც წყაროები ერთად გვაწვდიან, მეტია, ვიდრე მათი ინდივიდუალურად მოწოდებული ინფორმაციის ჯამი. მესამე ცვლადი მოქმედებს, როგორც დანარჩენ ორს შორის ურთიერთობის ხელშემწყობი.
უარყოფითი ურთიერთქმედების ინფორმაცია (< 0): ეს მიუთითებს სიჭარბის არსებობაზე. წყაროები ერთმანეთს ფარავენ სამიზნის შესახებ მოწოდებულ ინფორმაციაში, ამიტომ მათი გაერთიანებული ინფორმაცია ნაკლებია მათი ინდივიდუალური წვლილის ჯამზე. მესამე ცვლადი ხსნის ან ამცირებს დანარჩენ ორს შორის არსებულ კორელაციას.
ნულოვანი ურთიერთქმედების ინფორმაცია (= 0): ეს მიუთითებს, რომ წყაროები სამიზნის შესახებ ინფორმაციას დამოუკიდებლად გვაწვდიან.
ეს „მთელს გამოკლებული ჯამი“ მიდგომა არის ინტუიციური და გამოთვლითად მარტივი მეთოდი უმაღლესი რიგის ურთიერთქმედებების გამოსავლენად.[5]
2.4 კონტექსტუალიზაცია ნაწილობრივი ინფორმაციის დეკომპოზიციის (PID) ფარგლებში
მიუხედავად იმისა, რომ ურთიერთქმედების ინფორმაცია უმაღლესი რიგის ეფექტების მძლავრ, ერთ რიცხვში შეჯამებულ საზომს წარმოადგენს, უფრო ახალი და თეორიულად სრულყოფილი ჩარჩოა ნაწილობრივი ინფორმაციის დეკომპოზიცია (PID).[4, 7] PID-ის მიხედვით, მთლიანი ინფორმაცია, რომელსაც გაერთიანებული წყარო (\Sigma_1, \Sigma_2) გვაწვდის სამიზნე C-ს შესახებ, და რომელიც მოცემულია I(\Sigma_1, \Sigma_2; C)-ით, შეიძლება დაიშალოს ოთხ არაუარყოფით, განსხვავებულ კომპონენტად [2, 8]:
I(\Sigma_1, \Sigma_2; C) = R + U_1 + U_2 + S
სადაც:
R არის ჭარბი ინფორმაცია, რომელიც გაზიარებულია ორივე წყაროს მიერ.
U_1 არის უნიკალური ინფორმაცია, რომელიც მოწოდებულია მხოლოდ \Sigma_1-ის მიერ.
U_2 არის უნიკალური ინფორმაცია, რომელიც მოწოდებულია მხოლოდ \Sigma_2-ის მიერ.
S არის სინერგიული ინფორმაცია, რომელიც ხელმისაწვდომია მხოლოდ გაერთიანებული წყაროდან.
PID ჩარჩოს ფარგლებში, ინდივიდუალური ურთიერთინფორმაციის ტერმინები შედგება ამ ატომებისგან: I(\Sigma_1; C) = R + U_1 და I(\Sigma_2; C) = R + U_2. ეს საშუალებას გვაძლევს, უფრო ღრმად გავიგოთ VEGA LENS მეტრიკა. PID-ის განმარტებების ჩასმით ურთიერთქმედების ინფორმაციის ფორმულაში, ვლინდება მისი კავშირი PID ატომებთან:
\begin{align*}
\text{ურთიერთქმედების ინფორმაცია} &= I(\Sigma_1, \Sigma_2; C) - I(\Sigma_1; C) - I(\Sigma_2; C) \\
&= (R + U_1 + U_2 + S) - (R + U_1) - (R + U_2) \\
&= S - R
\end{align*}
ეს გამოყვანა კრიტიკულ შედეგს გვაძლევს: VEGA LENS ჩარჩოს მიერ გამოთვლილი მეტრიკა არ არის სინერგიის სუფთა საზომი PID-ის გაგ
This post has been edited by ვეგა on 1 Sep 2025, 13:28 

